2進数のかけ算・わり算
前回の記事では、2進数の四則演算のうち、【足し算と引き算】の計算方法を紹介しました。
今回は2進数の【かけ算とわり算】の計算方法についてお話ししていきたいと思います。
●まず10進数で考えてみよう
まずは、普段使用している10進数で考えてみましょう。
例として、「5000」という4桁の10進数があったとします。
これを10倍する時は
5000 × 10 = 50000
ですね。
また、1/10倍(÷10)する時は
5000 × 1/10 = 500
になります。
この計算を、今度は桁の動きに注目しながら
もうすこし詳しく紐解いていきましょう。
「5000」の桁についての表し方を
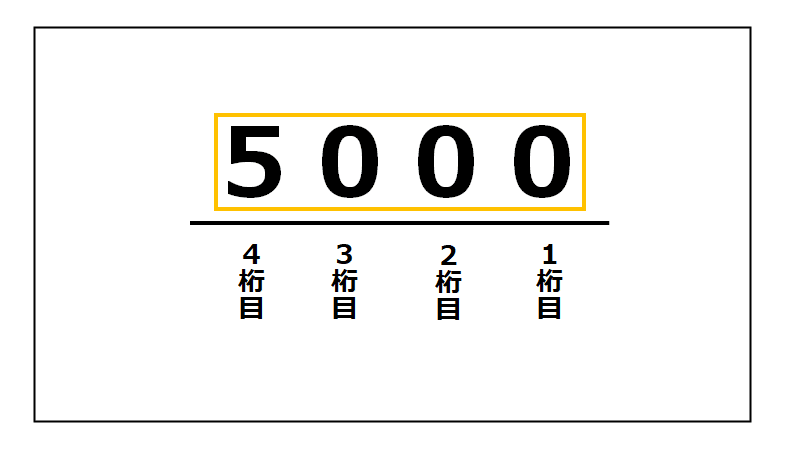
このようにしてみます。
※「5000」を、一つのかたまりとして認識して見てください。
10倍する時の桁の動きは・・・
桁の位置は固定して考えて、
①「5000」のかたまりを左に1つシフト
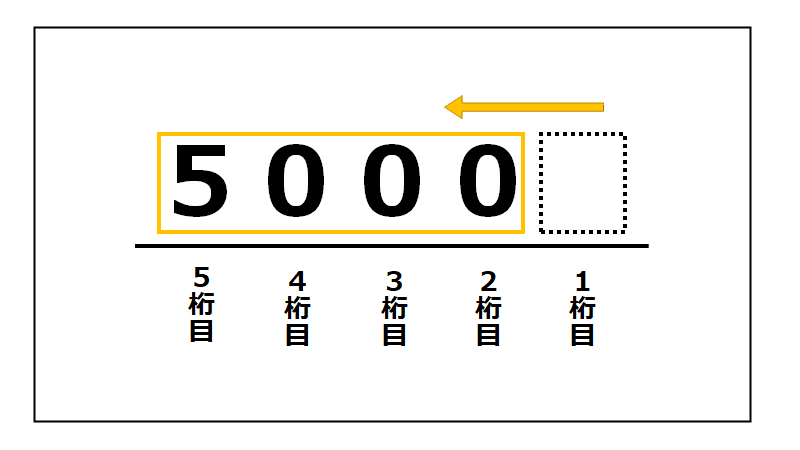
② 空いた1桁目に0を1つ入れる。
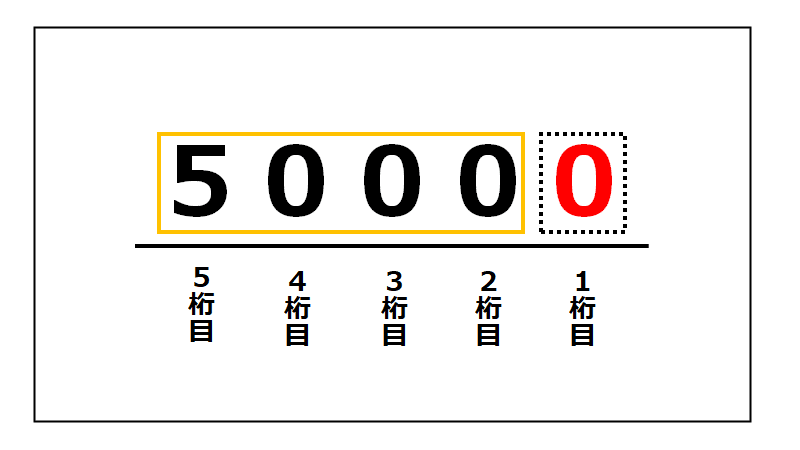
このようになります。
つまり、元の数字のかたまりを左に1つシフトすることによって、桁を1増やしています。
同じように、1/10倍する時の桁の動きは・・・
同様に桁の位置は固定して考えて、
①「5000」のかたまりを右に1つシフト
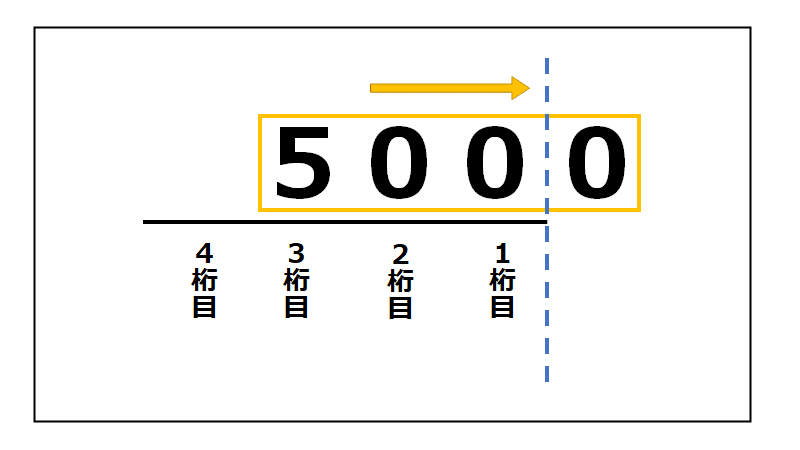
② ”1桁目”よりも右にある、元のかたまりの数字を消す
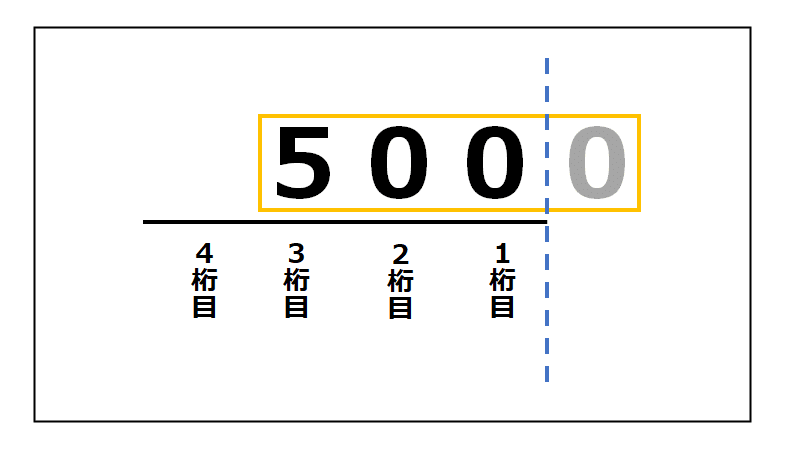
このようになります。
今度は右に1つシフトすることで、1桁減らしていますね。
つまり・・・
かけ算をする時は 【元となる数字のかたまりを左にシフトする】
わり算をする時は 【元となる数字のかたまりを右にシフトする】
という操作で行なうことができます。
●2進数に置き換えると
では、本題の2進数に置き換えて考えてみましょう!
例として、「110」という3桁の2進数があったとします。
10進数に直すと6です。(2進数から10進数の変換方法は前々回の記事参照)
では、先程の10進数で説明した考え方を使用して・・・
かけ算をする時は、どっちに動かすか覚えていますか?
・・・そう、左です。
①元の2進数の数字のかたまりを左に1つシフトします。
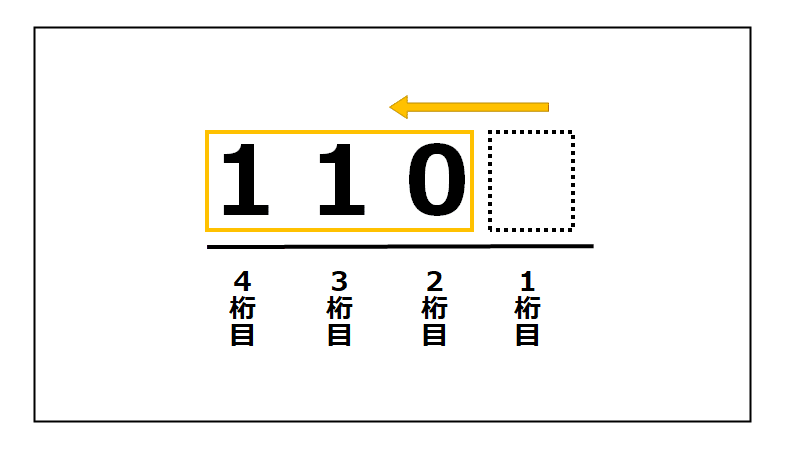
②空いた1桁目に0を1つ入れて・・・
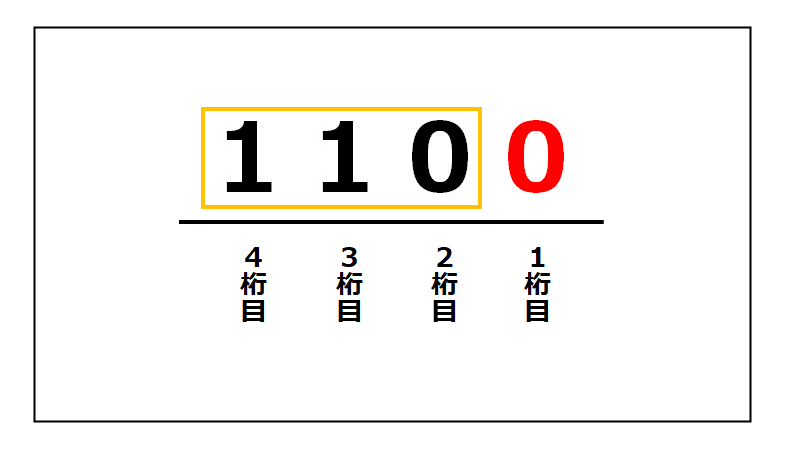
このように表すことができます。
元のかたまりを左に1シフトした結果、「1100」という数になりました。
これを10進数に直すと12となり、シフトする前の6の2倍になっています。
わり算も同じです。
①元の2進数の数字のかたまりを右に1つシフトします。
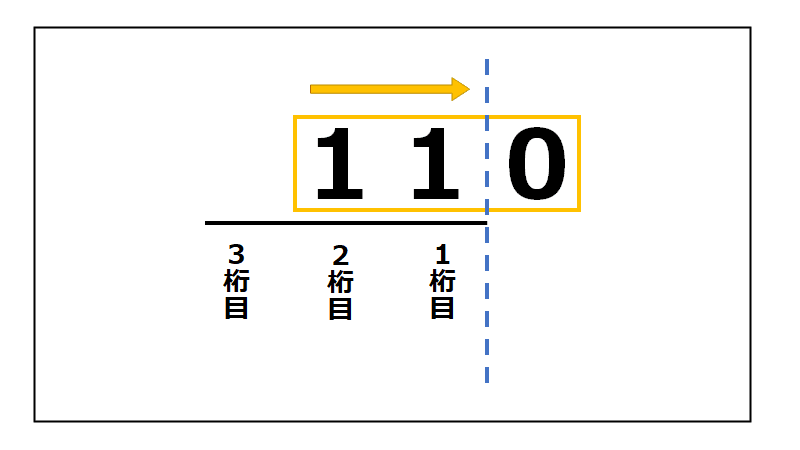
②”1桁目”よりも右にある、元のかたまりの数字を消します。
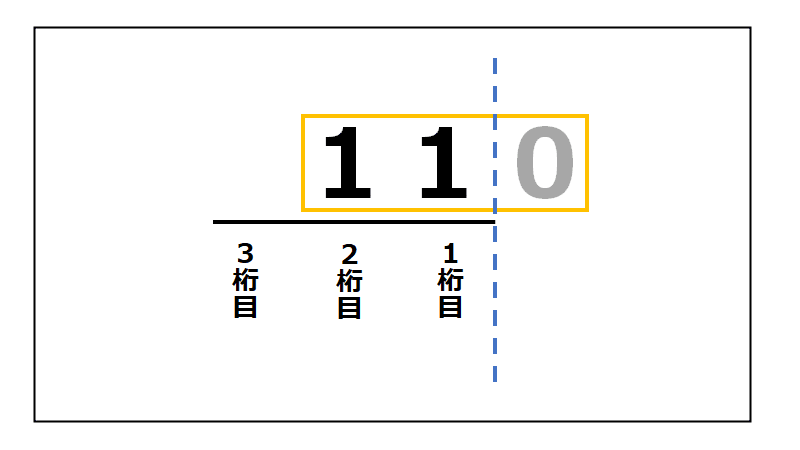
このように表すことができます。
元の数字のかたまりを右に1シフトした結果、「11」という数になりました。
これを10進数に直すと3となり、シフトする前の6の1/2倍になっています。
これが2進数のかけ算と、わり算の方法です。
また、この「2進数を左もしくは右にずらす操作」のことを
シフト演算と呼びます。
●論理シフトと算術シフト
先程ちらっと出てきた「シフト演算」という言葉ですが、
つまりは2進数のかけ算やわり算をする方法のことです。
このシフト演算には、種類があります。
見出しの通り、
「論理シフト」と「算術シフト」です。
2つの違いは、符号を考慮するかしないかです。
論理シフトは符号を考慮せずそのままシフト操作をします。
今まで上記で例として説明していたものは、すべて論理シフトのことでした。
(だって符号がどうとかは何も考えず、ただ左右にシフトしていましたよね!)
問題は算術シフトです。
こちらは、符号を考慮してシフト操作を行ないます。
・・・符号を考慮して行うシフト演算とは?なんぞや?
そう思った方がいて当然だと思います。筆者も同じことを思いました。
算術シフトの説明をする前に、前提知識を話しておきます。
そもそも、コンピュータは1と0を使用して動いています。
1と0、つまり2進数を組み合わせて、複雑な機能や動きを実現しているのです。
そんな2進数の1桁1桁を、1ビット(bit)と表したりします。
つまり、先程の2進数の例でいうと、
「110」は「3ビット」ということになります。
では、これらをふまえて、算術シフトの説明をしていきます!
●算術シフトを詳しく
符号を考慮するとは一体どういうことか。
それは、「先頭の符号ビットを固定にして、それ以降のビットだけを左右にシフト操作する」ということです。
・・・?
まだよくわかりませんね。
まず、算術シフトにおける符号ビットとは何か?
→ビットの集まりのうち、一番左のビットのことを、符号ビットと呼びます!
符号ビットが0だと正(+)、1だと負(-)という表現になります。
例えば、「11110100」という8ビットの2進数があるとします。
このうち、一番左の”1”は符号ビットとして固定し、それ以降の”1110100”について左や右にシフトする、というのが算術シフトです。
ちなみに「11110100」を10進数で表すと、-12となります。
それでは、「11110100」を2つ左に算術シフトしてみましょう。
①一番左を符号ビットとして固定
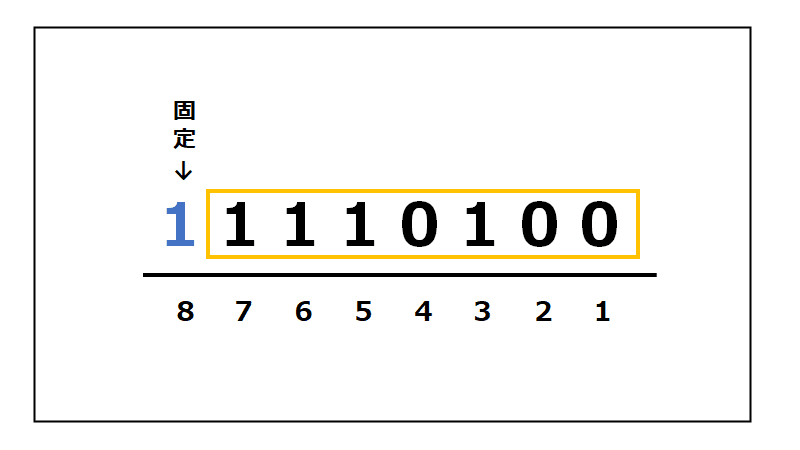
②符号ビットを除いた残り7ビットを2つ左シフト

③2シフトした分、空になった右のスペースに0を2つ入れ、8ビットよりあふれた左側の部分は削除
※ただし今回は、一番左は符号ビットで固定されているので、8ビット目に当たる部分も削除します。
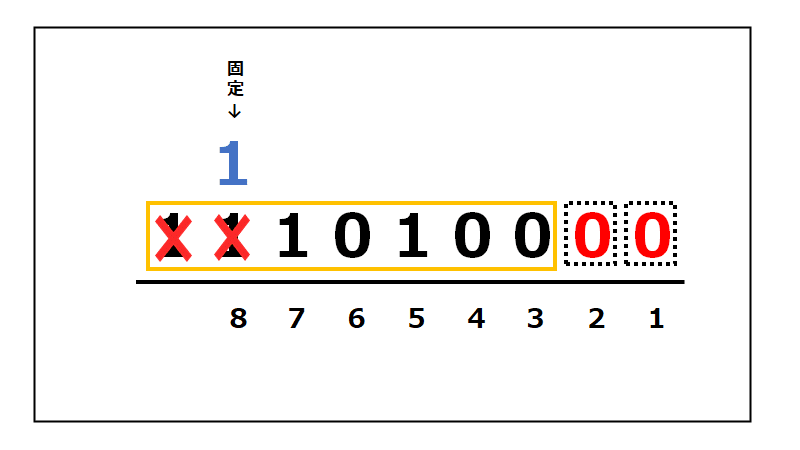
結果は以下のようになります! ↓↓↓
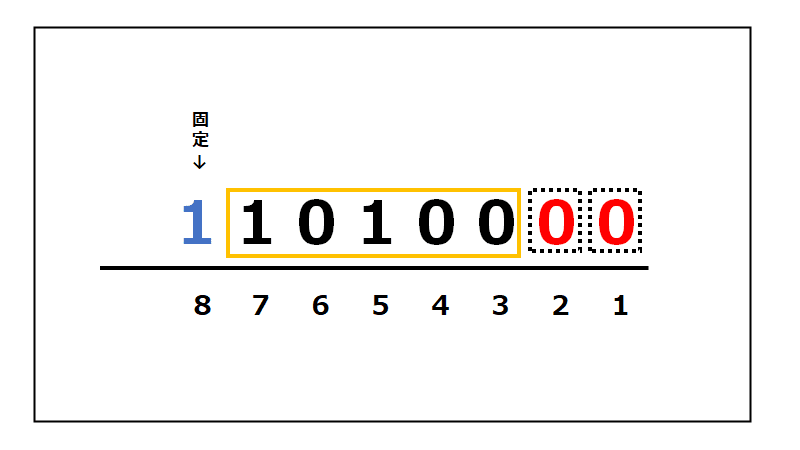
「11010000」になりました。
10進数に変換すると、-48となります。
元の-12の、符号を除いて2²倍=4倍となっていますね。
次に、2つ右に算術シフトしてみましょう。
①一番左を符号ビットとして固定
最初は左算術シフトの時と同じです。
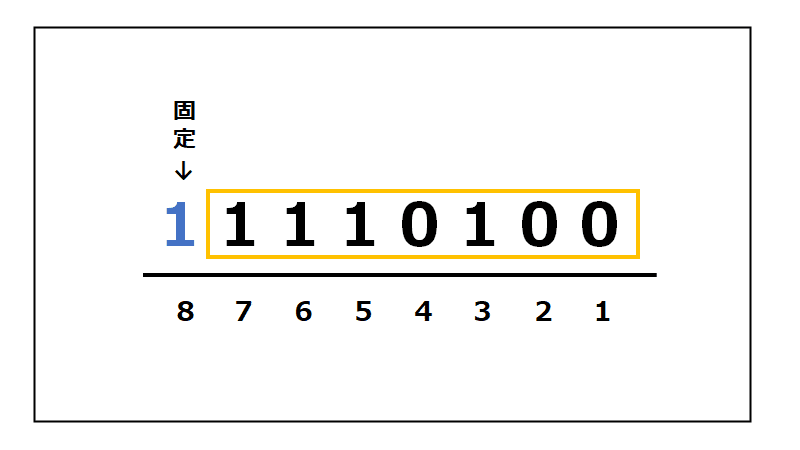
②符号ビットを除いた残り7ビットを2つ右シフト
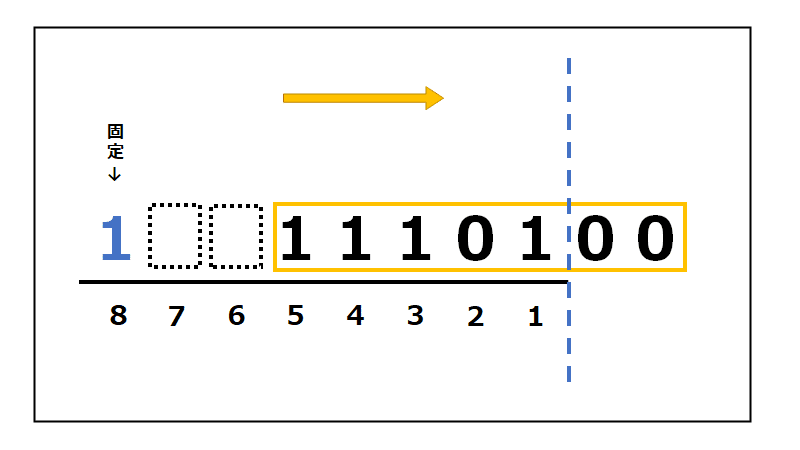
③”1桁目”より右にあふれた部分を削除。
空になった左側のスペースには、符号ビットと同じ数字を入れます。
今回は1なので、1を2つ入れます。
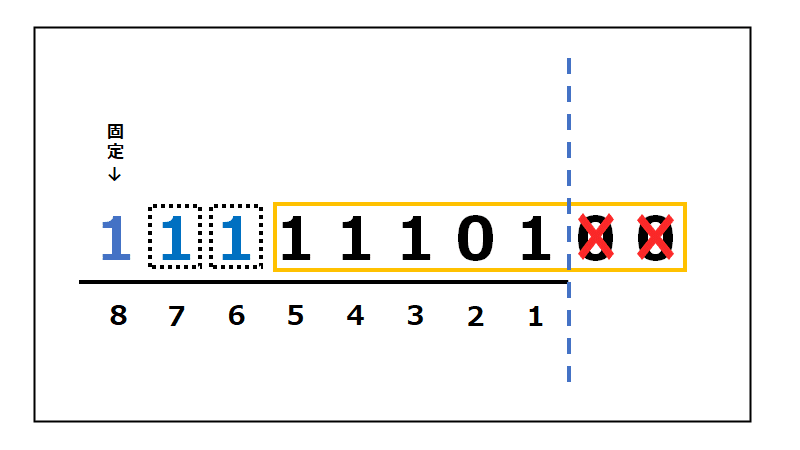
結果は以下のようになります! ↓↓↓
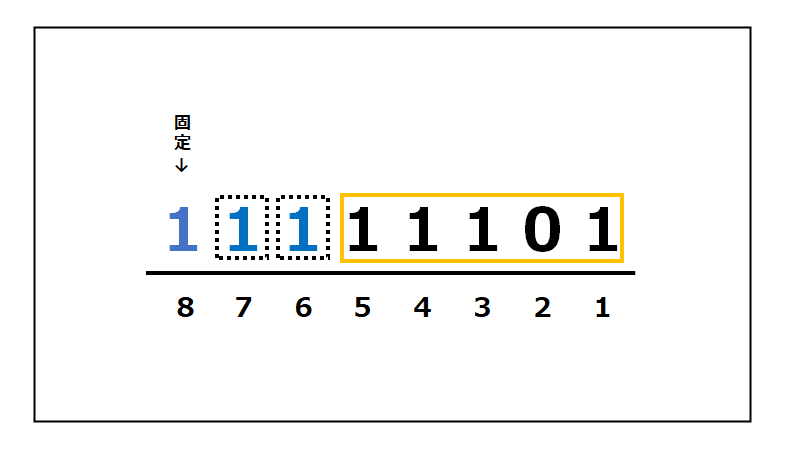
「11111101」になりました。
これを10進数に変換すると、-3。
おやおや、今度は元の-12の、符号を除き1/2^2倍=1/4倍となっています。
・・・もうお分かりですね。
論理シフトも算術シフトも共通ですが、
ずらしたビット数をnとすると
左シフト後の数は、元の数を「2のn乗」したものに、
右シフト後の数は、元の数を「1/2のn乗」したものになっています。
長くなりましたが、これが2進数の【かけ算とわり算】の基本的な考え方です。
●まとめ
・2進数はシフト演算という方法を用いて、かけ算やわり算を行う
・シフト演算には2種類ある
・論理シフトは符号ビットを考慮しないで普通にシフト操作する方式
・算術シフトは1番左のビットを符号ビットとして固定してシフト操作する方式
・論理シフトと算術シフトも共通して、
ずらしたビット数をnとすると
左シフト後の数は、元の数を「2のn乗」したものに、
右シフト後の数は、元の数を「1/2のn乗」したものになる
以上になります!
次回もお楽しみに。