小数を含む2進数
前回までの記事で、”整数”の2進数の四則演算を紹介してきました。
しかし、数の表し方は整数だけではありませんよね?
小数だったり、分数だったり…….
色々な数の表し方があります。
前回までの記事を読んだ方の中には、
2進数って小数も表せるのかな?
もし表せるのなら、どうやって計算するんだろう??
そんな疑問を持った人もいるかと思います。
そこでそれらの疑問を解決すべく、今回は「2進数の小数の表し方」と「小数の2進数の計算方法」に焦点を置いて解説していきたいと思っています!
●10進数を2進数に(小数編)
第1回の記事で10進数をn進数に直す方法についてご紹介しました。
しかし、整数に限った話だったので、今回は小数の10進数を、小数のn進数に直す方法をご紹介します!
小数部に関しても、ある法則があるので、まずは論理を抜きにして以下の法則をご覧ください。
10進数小数部をX、基数をBとする
①XをBで掛ける。この時、掛け算の結果の整数部をS、小数部をAとする。
➁Aが0なら変換処理を終え、求めたSを順に左から並べ、小数部が0でなければ、③の処理へ進む
③小数部AをXの新しい数とし、①の処理へ戻る
画像で表すとこんな感じ!
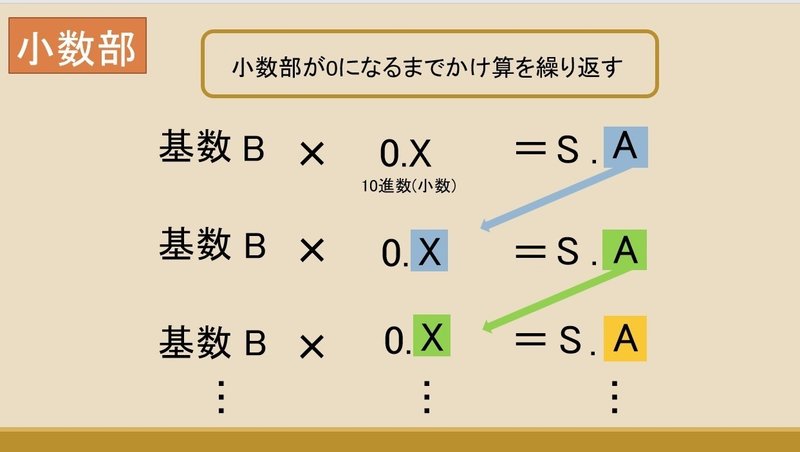
これだけは何を言ってるのか分からないと思うので、この法則に従って実際に10進数を2進数に直していきたいと思います。
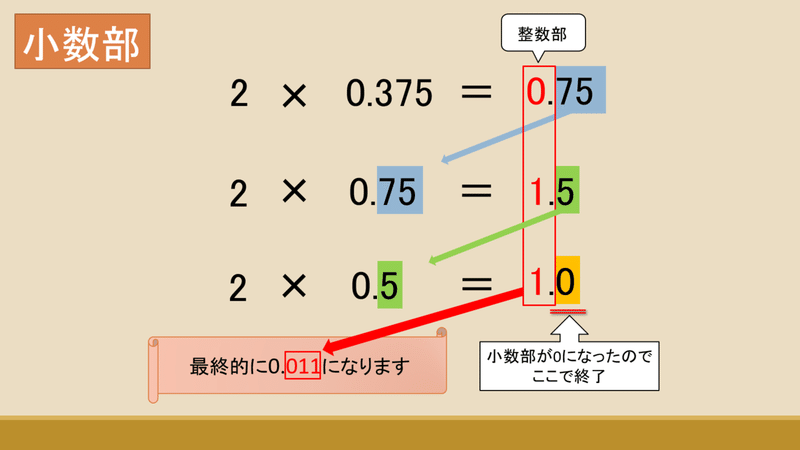
上から順に
0.375に2をかけて、整数部(0)と小数部(0.75)を出して、
次は小数部0.75に2をかけて、整数部(1)と小数部(0.5)を出して、
そのまた次も小数部0.5に2をかけて、整数部(1)と小数部(0.0)を出して、、、
と繰り返していって、小数部が0になるまで繰り返し、出てきた整数部を上から順に並べると2進数の小数部が完成します。
●2進数を10進数に(小数編)
では、次に2進数小数を10進数に直してみましょう。
こちらも第1回の記事でご紹介しました、数の重みに基づいて計算すると2進数を10進数にすることは簡単にできます。
復習もかねてもう一度おさらいします!!
10進数には以下のような特徴があります。
①1桁は0~9の有限の数字で表される。
②各桁は、左へ1桁進む度に10倍、右へ1桁進む度に1/10倍になる。
例えば10進数で123.45という数があった場合
123.45=1×10²+2×10¹+3×10⁰+4×10⁻¹+5×10⁻²
となります。
2進数も数そのものが持つ数の重みは変わらないため、10^x(10のx乗)の代わりに2^x(2のx乗)で分解していけばいいことになります。
例えば、2進数で0.011と表される数があったとします。
この場合、分解して考えると
0.011(2進数)=0×2⁻¹+1×2⁻²+1×2⁻³
=0+0.25+0.125
=0.375(10進数)
となります。
先ほど紹介した10進数の0.375を2進数に直した結果と一致しますので、成り立つと言えます!
●小数点を含む10進数の計算
それでは、ここからは具体的な計算を少しだけ見ていきましょう。
説明が難しくなってしまうので四則演算のうち加法に限って今回はお話していきます。
例えば
0.5+0.5
という10進数小数の計算があったとします。
第2回目の記事でもご紹介した通り、10進数で桁上がりするのは、もちろん、10になってからですよね。しかし、それは10進数が0~9までの数字で表されていて、10より大きな数を表す的確な1文字の数が無いからです。よって9より大きい数字を表すときは左に桁を添えていきます。
この原理に沿って考えていくと、
0.5+0.5=1.0
と桁が上がることが分かります。
この記事を読んでいる(2進数の勉強をしている)あなたなら、深く考えずとも簡単に答えられるかと思います!
●小数点を含む2進数の計算
いよいよこの記事の本題である、小数点を含む2進数の計算についてお話ししていきます。
まずは、小数を含む10進数を2進数に直す手段を使って0.5(10進数)を2進数に直していきたいと思います。
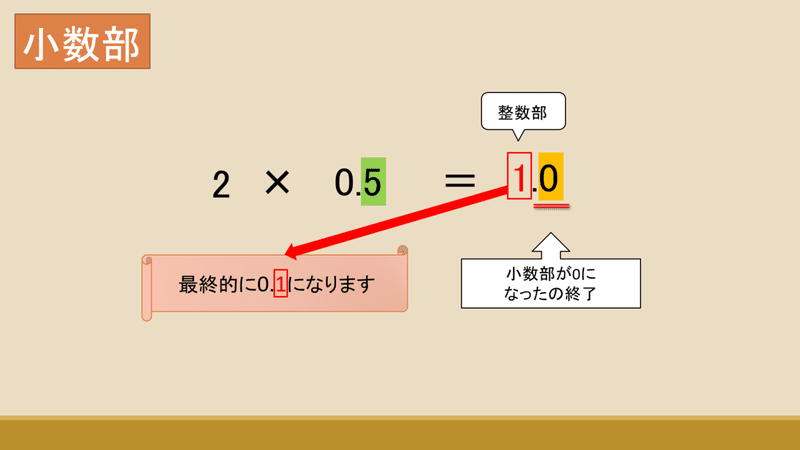
よって、0.5(10進数)=0.1(2進数)
ということが分かりました!
ここで、0.1(2進数)+0.1(2進数)の計算をしてみましょう。
答えは0.2でしょうか??
いいえ、答えは1.0になります!
これも10進数と原理は一緒です。
2進数は0と1という2つの数しか存在せず、それ以上の数字は存在しません。だから2という数字は一桁で表せません。
そこで、左に桁を添えて、元の位を0に戻して表すのです。
つまり
0.1(2進数)+0.1(2進数)=1.0(2進数)
となります。
2進数で表された1.0と10進数で表された1.0は数の重みが等しい(同じ数!)ので、この計算結果は、前述した10進数の計算結果と一致すると言えます!!
まとめ
・小数点を含む10進数を2進数に直す方法
→小数部が0になるまで掛け算を繰返し、掛け算の結果の整数部を順に並べる。
・小数点を含む2進数を10進数に直す方法
→2^x(2のx乗)で分解して、その結果を全て加算する(小数点を含まない場合と同じ!)。
・小数点を含む2進数の計算
→桁上がりのタイミングが9の次ではなく、1の次になる以外は、基本的には、10進数の計算と同じ!
長くなりましたが、今回はここまで。
次回もお楽しみに!



